Algebraic Topology: A Detailed Exploration for You
Algebraic topology is a fascinating branch of mathematics that intertwines algebra and topology to study the properties of spaces. It’s a field that has intrigued mathematicians for centuries, and its concepts are now widely used in various scientific and engineering disciplines. In this article, I will delve into the intricacies of algebraic topology, providing you with a comprehensive understanding of its key ideas and applications.
What is Algebraic Topology?
Algebraic topology is the study of topological spaces using algebraic structures. It aims to classify and understand the properties of spaces by associating algebraic invariants to them. These invariants are functions that assign algebraic objects to topological spaces, and they help us understand the structure of these spaces.
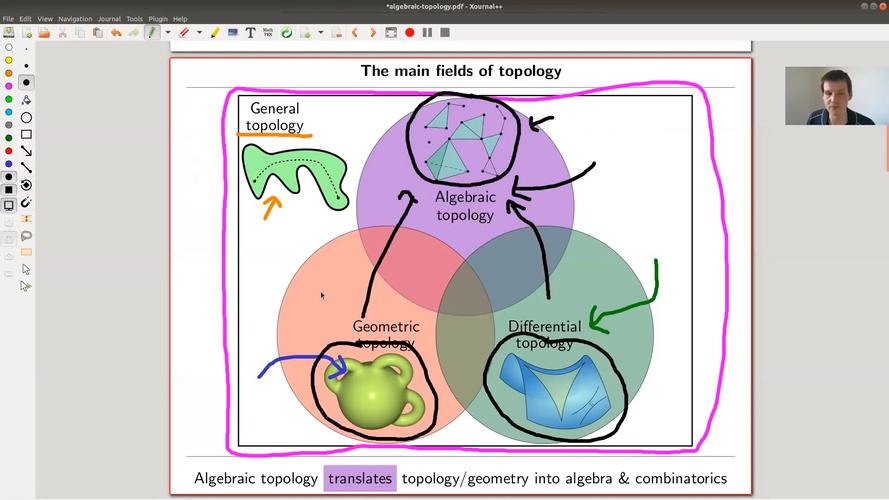
One of the most fundamental concepts in algebraic topology is the notion of a homotopy. A homotopy is a continuous deformation of one space into another. This idea allows us to compare spaces and determine whether they are “the same” in some sense. If two spaces can be continuously deformed into each other, they are said to be homotopy equivalent.
Algebraic Invariants
Algebraic invariants are essential tools in algebraic topology. They provide a way to measure the “shape” of a space. Some common algebraic invariants include the fundamental group, homology groups, and cohomology groups.
The fundamental group, often denoted as 蟺鈧?X), is a group that captures the information about loops in a space. It consists of all continuous loops based at a single point, along with the operation of concatenation. The fundamental group is a powerful tool for understanding the connectivity of a space. For example, a space is simply connected if its fundamental group is trivial (i.e., it has only one element).
Homology groups are another important algebraic invariant. They are constructed from the cycles and boundaries in a space. A cycle is a closed loop that does not intersect itself, while a boundary is the boundary of a region in the space. The homology groups provide information about the number of “holes” in a space. For instance, the first homology group, H鈧?X), counts the number of connected components in a space.

Cohomology groups are the duals of homology groups. They are constructed from the cochains and cocycles in a space. Cohomology groups provide information about the “holes” in the homology groups. For example, the first cohomology group, H1(X), counts the number of independent cycles in a space.
Applications of Algebraic Topology
Algebraic topology has found numerous applications in various fields. Here are a few examples:
| Field | Application |
|---|---|
| Physics | Understanding the topology of spacetime and the behavior of particles |
| Computer Science | Designing algorithms for image processing, data analysis, and machine learning |
| Biology | Studying the structure and function of biological molecules and cells |
| Engineering | Optimizing designs and materials, and understanding the behavior of complex systems |
In physics, algebraic topology helps us understand the topology of spacetime and the behavior of particles. In computer science, it is used to design algorithms for image processing, data analysis, and machine learning. In biology, it aids in studying the structure and function of biological molecules and cells. And in engineering, it helps optimize designs and materials, as well as understand the behavior of complex systems.
Conclusion
Algebraic topology is a rich and diverse field that has the power to transform our understanding of the world. By combining algebra and topology, it provides us with a unique perspective on the properties of spaces. Whether you are a mathematician, physicist, engineer, or computer scientist, the concepts of algebraic topology are sure to enrich your knowledge and inspire new ideas.





